Tmap and Assorted Work
Linear Relationship: GNP and LEXPF - country_demographics.csv
Correlation coefficient between GNP and LEXPF
# set working directory
setwd("C:/Users/data")
country<-read.csv("country_demographics.csv",sep=",",header=T)
country2<-country[complete.cases(country), ]
countryDF<-as.data.frame(country2)
LEXPF<-countryDF$LEXPF
GNP<-countryDF$GNP
str(LEXPF)## num [1:91] 75.5 74.7 77.7 73.8 75.7 72.4 74 75.9 74.8 72.7 ...str(GNP)## int [1:91] 600 2250 2980 2780 1690 1640 2242 1880 1320 2370 ...cor(GNP,LEXPF)## [1] 0.6500464Correlation coefficient, rather than covariance, is the first step in determining the linear relationship between gross national product and the life expectancy of females in the country demographics data set due to impact that variable scales have on covariance values. The correlation coefficient evidences the magnitude of the association between variables on a scale of -1 to 1. The correlation coefficient value is generated using the covariance of the variables and dividing that value by the value of each variables’ standard deviation multiplied by one another. The correlation coefficient for the country_demographics data set is 0.6500464. This value is positive and closer to 1 than it is to 0 suggesting a strong positive relationship. The regression model and t* test-statistic for significance will indicate more about the relationship.
Set hypothesis statement as:
H_0: p = 0
H_A: p != 0
lm<-lm(LEXPF~GNP)
lm##
## Call:
## lm(formula = LEXPF ~ GNP)
##
## Coefficients:
## (Intercept) GNP
## 6.09e+01 8.94e-04summary(lm)##
## Call:
## lm(formula = LEXPF ~ GNP)
##
## Residuals:
## Min 1Q Median 3Q Max
## -19.8771 -5.8096 0.6023 6.5539 14.1377
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.090e+01 1.095e+00 55.60 < 2e-16 ***
## GNP 8.940e-04 1.108e-04 8.07 3.12e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.506 on 89 degrees of freedom
## Multiple R-squared: 0.4226, Adjusted R-squared: 0.4161
## F-statistic: 65.13 on 1 and 89 DF, p-value: 3.118e-12The p-value of 3.118e-12, or 0.000000000003118, is less than the significance level of 0.05. Therefore, the null hypothesis is rejected. Additionally, the coefficients tell us that for every one unit increase in gross national product, there is an 8.940e-04 (or 0.0008940) increase in female life expectancy. Interpretation of these are results using y=mx+b formula is y=0.0008940(x)+60.90. This tells us that with a GNP of $0 the female life expectancy is 60.90 years (variable b in the equation). For each additional unit of GNP, female life expectancy increases by 0.0008940 years (variable m in the equation, also known as the slope).
Plotting the Relationship: GNP and LEXPF
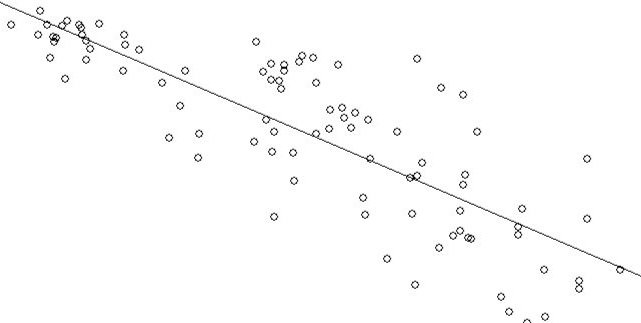
plot(GNP,LEXPF)
abline(lm(LEXPF~GNP))The plot is positively skewed. Let’s look at the plot for this relationship and the accompanying regression line while using log(). Log() will reduce the skew produced by the GNP variable by pulling in outlier values that cause the skew seen in the plot above.
Plotting the Relationship: GNP and LEXPF with log()
logGNP<-log(GNP)
plot(logGNP,LEXPF)
abline(lm(LEXPF~logGNP))The log() function generated a distribution that is closer to a normal distribution and appears less impacted by skew than the previous plot. From the new plot we can see that the value of b in y=mx+b has decreased significantly, suggestion that the analysis done prior to the log() function was impacted by the skew present in the GNP data.
Recalculating the Correlation Coefficient using the Logged GNP
cor(logGNP,LEXPF)## [1] 0.8233949The correlation coefficient value of the relationship, using the logged GNP data, is 0.08233949. This value suggests that the data is more strongly positively correlated than the previous calculation indicated.
Working with Shapefiles
Data Sources: U.S. Census 5-Digit ZIP Code Tabulation Area (ZCTA 5) 2000 - 2019 (Social Explorer). / Colleges and Universities (HIFLD Open Data).
Load Libraries and Shapefiles
library(tmap)
library(tmaptools)
library(raster)library(sf)setwd("C:/Users/data")
counties<-st_read("tl_2022_us_county.shp")## Reading layer `tl_2022_us_county' from data source
## `C:\Users\data\tl_2022_us_county.shp'
## using driver `ESRI Shapefile'
## Simple feature collection with 3235 features and 17 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -179.2311 ymin: -14.60181 xmax: 179.8597 ymax: 71.43979
## Geodetic CRS: NAD83colleges<-st_read("CollegesUniversities.shp")## Reading layer `CollegesUniversities' from data source
## `C:\Users\data\CollegesUniversities.shp'
## using driver `ESRI Shapefile'
## Simple feature collection with 6559 features and 43 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: -19007040 ymin: -1611319 xmax: 19077760 ymax: 11514220
## Projected CRS: WGS 84 / Pseudo-MercatorFilter Data Sets for California
The CA Counties shapefile mapped by land area in square meters allows the viewer to visualize counties with the largest area. This visualization shows that California counties with the largest area tend to be clustered in the inland desert portion of the state with two large area counties residing in the northern region of the state.
countiesCA <- counties[counties$STATEFP == '06', ]
collegesCA <- colleges[colleges$STATE == 'CA', ]Map CA Counties using ALAND Variable
tmap_options(check.and.fix = TRUE)
tm_shape(countiesCA)+tm_fill("ALAND", title="Sq. M Area", style = "quantile", n=8, palette = "Blues")+tm_borders()+tm_compass(position = c("LEFT", "BOTTOM"))+tm_layout(main.title = "CA Counties & Area", legend.position = c("RIGHT", "TOP"), title.position = c("center", "top"), inner.margins = .01)+tm_scale_bar(position = c("LEFT", "BOTTOM"))Map Colleges and CA Counties using ALAND Variable
tm_shape(countiesCA)+tm_fill("ALAND", title="Sq. M Area", style = "quantile", n=8, palette = "Blues")+tm_borders()+tm_compass(position = c("LEFT", "BOTTOM"))+tm_layout(main.title = "CA Counties & Colleges", main.title.size = 1, legend.outside = TRUE, legend.outside.position = "bottom", main.title.position = "LEFT")+tm_scale_bar(position = c("LEFT", "BOTTOM")) + tm_shape(collegesCA) + tm_dots(col = "POPULATION", palette = "Greens", style = "quantile", title = "College Population Size", size = .05)Point Pattern Analysis
# mean center
xy<-cbind(collegesCA$LONGITUDE, collegesCA$LATITUDE)
mc<-apply(xy, 2, mean)
mcCA<-st_sfc(st_point(c(mc[1],mc[2])))
mcCA## Geometry set for 1 feature
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: -119.2307 ymin: 35.28371 xmax: -119.2307 ymax: 35.28371
## CRS: NA## POINT (-119.2307 35.28371)tm_shape(countiesCA)+tm_fill("ALAND", title="Sq. M Area", style = "quantile", n=8, palette = "Blues")+tm_borders()+tm_compass(position = c("LEFT", "BOTTOM"))+tm_layout(main.title = "CA Counties & Colleges", main.title.size = 1, legend.outside = TRUE, legend.outside.position = "bottom", main.title.position = "LEFT")+tm_scale_bar(position = c("LEFT", "BOTTOM")) + tm_shape(collegesCA) + tm_dots(col = "POPULATION", palette = "Greens", style = "quantile", title = "College Population Size", size = .05) + tm_shape(mcCA) + tm_dots(col='red',size=.35)# mean circle
sd<-sqrt(sum((xy[,1] - mc[1])^2 + (xy[,2] - mc[2])^2) / nrow(xy))
bearing<-1:360 * pi/180
cx<-mc[1]+sd*cos(bearing)
cy<-mc[2]+sd*sin(bearing)
circle<-cbind(cx, cy)
mean_circle<-st_sfc(st_multipoint(circle))
tm_shape(countiesCA)+tm_fill("ALAND", title="Sq. M Area", style = "quantile", n=8, palette = "Blues")+tm_borders()+tm_compass(position = c("LEFT", "BOTTOM"))+tm_layout(main.title = "CA Counties & Colleges", main.title.size = 1, legend.outside = TRUE, legend.outside.position = "bottom", main.title.position = "LEFT")+tm_scale_bar(position = c("LEFT", "BOTTOM")) + tm_shape(collegesCA) + tm_dots(col = "POPULATION", palette = "Greens", style = "quantile", title = "College Population Size", size = .05) + tm_shape(mcCA) + tm_dots(col='red',size=.35) + tm_shape(mean_circle) + tm_dots(col='red',shape=21)The spatial mean center is calculated by adding all x values together and dividing that value by the total number of observations in the calculation; the same calculation is done with the y values. The result is an average, or mean, coordinate that represents the center of the data. The mean center of the CA Counties and Colleges data is -119.2307, 35.28371 and tells viewers that the average of the coordinate positions resides in Central California, just above the South Coast region.The location suggests that a large number of the California Colleges reside in the Southern coastal region of the state with the next largest density of colleges occurring in the Bay Area region. These high densities result in the mean center residing between the Bay Area and Southern Coast regions of California while remaining closer to the southern portion due to the higher density of colleges in that region.
State Population and Centroids Data Sets
Data Sources: U.S. States and Territories (National Weather Service & NOAA).
Load the Data Sets
setwd("C:/Users/data")
pop<-read.csv("us_state_popln_history.csv",sep=",",header=T)
centroids<-read.csv("us_state_centroids.csv",sep=",",header=T)
states<-st_read("tl_2017_us_state.shp")## Reading layer `tl_2017_us_state' from data source
## `C:\Users\data\tl_2017_us_state.shp'
## using driver `ESRI Shapefile'
## Simple feature collection with 56 features and 14 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -179.2311 ymin: -14.60181 xmax: 179.8597 ymax: 71.43979
## Geodetic CRS: NAD83Filter Data Sets
pop2 <- pop[which(pop$state !="Alaska" & pop$state !="Hawaii"),]
states2 <- states[which(states$NAME !="Alaska" & states$NAME !="Hawaii" & states$NAME !="Commonwealth of the Northern Mariana Islands" & states$NAME !="American Samoa" & states$NAME !="Puerto Rico" & states$NAME !="United States Virgin Islands" & states$NAME !="Guam"), ]Dealing with NA Values
In order to deal with the two NA values present in the Oklahoma data for 1870 and 1880, we are going to set NA values to 0 for the calculation of the weighted mean center as missing values will produce an error.
Merging Population Data and the State Shapefile
stpop <- merge(states2, pop2, by.x="NAME", by.y="state")## NAME REGION DIVISION STATEFP
## Length:49 Length:49 Length:49 Length:49
## Class :character Class :character Class :character Class :character
## Mode :character Mode :character Mode :character Mode :character
##
##
##
## STATENS GEOID STUSPS LSAD
## Length:49 Length:49 Length:49 Length:49
## Class :character Class :character Class :character Class :character
## Mode :character Mode :character Mode :character Mode :character
##
##
##
## MTFCC FUNCSTAT ALAND AWATER
## Length:49 Length:49 Min. :1.584e+08 Min. :1.868e+07
## Class :character Class :character 1st Qu.:9.279e+10 1st Qu.:1.540e+09
## Mode :character Mode :character Median :1.389e+11 Median :3.543e+09
## Mean :1.562e+11 Mean :8.744e+09
## 3rd Qu.:2.062e+11 3rd Qu.:8.532e+09
## Max. :6.766e+11 Max. :1.040e+11 ## INTPTLAT INTPTLON pop1870 pop1880
## Length:49 Length:49 Min. : 0 Min. : 0
## Class :character Class :character 1st Qu.: 91874 1st Qu.: 174768
## Mode :character Mode :character Median : 537454 Median : 802525
## Mean : 786915 Mean :1023587
## 3rd Qu.:1184059 3rd Qu.:1542180
## Max. :4382759 Max. :5082871
## pop1890 pop1900 pop1910 pop1930
## Min. : 47355 Min. : 42335 Min. : 81875 Min. : 91058
## 1st Qu.: 332422 1st Qu.: 411588 1st Qu.: 577056 1st Qu.: 687497
## Median :1118588 Median :1311564 Median :1574449 Median : 1854482
## Mean :1284647 Mean :1550910 Mean :1876985 Mean : 2505613
## 3rd Qu.:1767518 3rd Qu.:2069042 3rd Qu.:2333860 3rd Qu.: 2939006
## Max. :6003174 Max. :7268894 Max. :9113614 Max. :12588066 ## pop1940 pop1950 pop1960 pop1970
## Min. : 110247 Min. : 160083 Min. : 285278 Min. : 332416
## 1st Qu.: 663091 1st Qu.: 791896 1st Qu.: 951023 1st Qu.: 1016000
## Median : 1901974 Median : 2233351 Median : 2535234 Median : 2824376
## Mean : 2687128 Mean : 3075456 Mean : 3642127 Mean : 4125367
## 3rd Qu.: 3137587 3rd Qu.: 3444578 3rd Qu.: 4319813 3rd Qu.: 4676501
## Max. :13479142 Max. :14830192 Max. :16782304 Max. :19953134 ## pop1980 pop1990 pop2000 pop2010
## Min. : 469557 Min. : 453588 Min. : 493782 Min. : 563626
## 1st Qu.: 1302894 1st Qu.: 1515069 1st Qu.: 1808344 1st Qu.: 1852994
## Median : 3107576 Median : 3486703 Median : 4041769 Median : 4533372
## Mean : 4595495 Mean : 5041869 Mean : 5705784 Mean : 6258674
## 3rd Qu.: 5463105 3rd Qu.: 6016425 3rd Qu.: 6349097 3rd Qu.: 6724540
## Max. :23667902 Max. :29760021 Max. :33871648 Max. :37253956 ## pop2020 lon lat geometry
## Min. : 576851 Min. :-120.56 Min. :28.63 MULTIPOLYGON :49
## 1st Qu.: 1961504 1st Qu.:-100.23 1st Qu.:35.86 epsg:4269 : 0
## Median : 4657757 Median : -89.20 Median :39.33 +proj=long...: 0
## Mean : 6719604 Mean : -90.99 Mean :39.50
## 3rd Qu.: 7705281 3rd Qu.: -78.85 3rd Qu.:43.00
## Max. :39538223 Max. : -69.24 Max. :47.45Weighted Mean Center
x<-stpop2$lon
y<-stpop2$lat
wmx_1870<-weighted.mean(x,stpop2$pop1870)
wmy_1870<-weighted.mean(y,stpop2$pop1870)
wmx_1880<-weighted.mean(x,stpop2$pop1880)
wmy_1880<-weighted.mean(y,stpop2$pop1880)
wmx_1890<-weighted.mean(x,stpop2$pop1890)
wmy_1890<-weighted.mean(y,stpop2$pop1890)
wmx_1900<-weighted.mean(x,stpop2$pop1900)
wmy_1900<-weighted.mean(y,stpop2$pop1900)
wmx_1910<-weighted.mean(x,stpop2$pop1910)
wmy_1910<-weighted.mean(y,stpop2$pop1910)
wmx_1930<-weighted.mean(x,stpop2$pop1930)
wmy_1930<-weighted.mean(y,stpop2$pop1930)
wmx_1940<-weighted.mean(x,stpop2$pop1940)
wmy_1940<-weighted.mean(y,stpop2$pop1940)
wmx_1950<-weighted.mean(x,stpop2$pop1950)
wmy_1950<-weighted.mean(y,stpop2$pop1950)
wmx_1960<-weighted.mean(x,stpop2$pop1960)
wmy_1960<-weighted.mean(y,stpop2$pop1960)
wmx_1970<-weighted.mean(x,stpop2$pop1970)
wmy_1970<-weighted.mean(y,stpop2$pop1970)
wmx_1980<-weighted.mean(x,stpop2$pop1980)
wmy_1980<-weighted.mean(y,stpop2$pop1980)
wmx_1990<-weighted.mean(x,stpop2$pop1990)
wmy_1990<-weighted.mean(y,stpop2$pop1990)
wmx_2000<-weighted.mean(x,stpop2$pop2000)
wmy_2000<-weighted.mean(y,stpop2$pop2000)
wmx_2010<-weighted.mean(x,stpop2$pop2010)
wmy_2010<-weighted.mean(y,stpop2$pop2010)
wmx_2020<-weighted.mean(x,stpop2$pop2020)
wmy_2020<-weighted.mean(y,stpop2$pop2020)
wm_x <- c(wmx_1870, wmx_1880, wmx_1890, wmx_1900, wmx_1910, wmx_1930,wmx_1940, wmx_1950, wmx_1960, wmx_1970, wmx_1980, wmx_1990, wmx_2000, wmx_2010, wmx_2020)
wm_y<-c(wmx_1870, wmx_1880, wmx_1890, wmx_1900, wmx_1910, wmx_1930,wmx_1940, wmx_1950, wmx_1960, wmx_1970, wmx_1980, wmx_1990, wmx_2000, wmx_2010, wmx_2020)
wm_xy<-cbind(wm_x,wm_y)
df_wmxy<-data.frame(wm_xy)
uspoints<-st_as_sf(x=df_wmxy,coords=c("wm_x","wm_y"),crs=4326)
# uspoints2<- st_transform(uspoints, crs = "+proj=longlat +datum=NAD83") # tried this but it did not help
years<-c("1870", "1880", "1890", "1900", "1910", "1930", "1940", "1950", "1960", "1970", "1980", "1990", "2000", "2010", "2020")
uspointsYears<-cbind(uspoints,years)Mapping Weighted Means
tm_shape(stpop2)+tm_polygons()+
tm_shape(uspointsYears)+tm_dots()stpop2 <- merge(stpop, centroids, by.x="NAME", by.y="state")
stpop2[is.na(stpop2)] = 0
summary(stpop2)